複雑そうな計算式は用いずにイメージしやすいようにした。
「ライトが光を発し」、「光が物体に当たり」、「物体から反射した光を見る」 といった現象を明るさの単位で分けられる
| 光度 | 「ライトが光を発し」 | どの方向にどのくらい光が出ているのかライトの強度を示す |
| 照度 | 「光が物体に当たり」 | その場所が明るいのかどうか、どれだけの光を受けているかを示す |
| 輝度 | 「物から反射した光を見る」 | 反射の結果、着目した部分が人の目にどれだけ光が来るのか、どのくらいの明るさで映るのかを示す |
「光束」とはこれらの単位の基となっている。
上で適当に選んだ色を数値として比べるとこれだけ差がある
光の単位は明るさを意味するのだが光は電磁波であり、人が見える部分だけを抜き出したものなので、「明るさ」とは「人間の見える部分だけ」というフィルターがかかっている。
「測光量」と「放射量」
「放射量:radiometric」とは光が持つエネルギー量を扱う物理量。W(ワット)、j(ジュール)等。
「測光量:photometric」とは人が感じる光だけを対象としたいので波長に重みを付けた量。lm(ルーメン)、lx(ルクス)等。
人は電磁波の一部しか見えない
人は狭い範囲の電磁波しか見えず、黄緑色に相当する555nmの波長を一番明るく感じ、そこから離れると感度が弱まり紫外線や赤外線では全く見えない。
人に見える電磁波のことを「可視光」と区分している。
「可視光」は380~780nmの区間と言われているが文献によって最低360nm、最大830nmのものもある。
赤外線や紫外線は人には見えないが紫外線は日焼けや殺菌等の化学変化を起こすほど強いエネルギーがある。
「明るさ」に紫外線や赤外線まで含めて扱ってしまうと見えないのに数値上は明るいといことになってしまうので人間の感度フィルターを適用する必要があり、このフィルターが 「比視感度」と呼ばれるものである。
人に見える電磁波のことを「可視光」と区分している。
「可視光」は380~780nmの区間と言われているが文献によって最低360nm、最大830nmのものもある。
赤外線や紫外線は人には見えないが紫外線は日焼けや殺菌等の化学変化を起こすほど強いエネルギーがある。
「明るさ」に紫外線や赤外線まで含めて扱ってしまうと見えないのに数値上は明るいといことになってしまうので人間の感度フィルターを適用する必要があり、このフィルターが 「比視感度」と呼ばれるものである。
「比視感度」は放射量と測光量の橋渡しをするものでもある。
このようなヒトの特性に合わせた量の全般を「心理物理量」と呼ばれその中でも光に関しては「測光量」と呼ばれている。
緑と青があった場合、放射量が同じなら緑は青よりも明るく感じる。
測光量が同じなら青も緑も同じ明るさに感じる。
このようなヒトの特性に合わせた量の全般を「心理物理量」と呼ばれその中でも光に関しては「測光量」と呼ばれている。
緑と青があった場合、放射量が同じなら緑は青よりも明るく感じる。
測光量が同じなら青も緑も同じ明るさに感じる。
人は3原色
人が見える電磁波の波長の最短と最長の比率は2倍程度しかない。
自然界に色が直接あるわけではなく、反応する感度をずらした3種類の錐体(L,M,S錐体)が受けた刺激の比率で脳が色を作り出しカラフルにみていることになる。
そのため物理的な波長が異なっても刺激の割合が同じなら同じ色として認識してしまう。
動物は4原色で色を認識するものが多く、対応する波長の範囲も人間より広い。
哺乳類は色に乏しく2原色だが霊長類は少しいびつではあるが3原色を獲得している。
天体観測ではガンマ線、X線、紫外線、赤外線、電波を撮影し、波長を少しずらした3成分を合成して無理やり色として人に見せている。
自然界に色が直接あるわけではなく、反応する感度をずらした3種類の錐体(L,M,S錐体)が受けた刺激の比率で脳が色を作り出しカラフルにみていることになる。
そのため物理的な波長が異なっても刺激の割合が同じなら同じ色として認識してしまう。
動物は4原色で色を認識するものが多く、対応する波長の範囲も人間より広い。
哺乳類は色に乏しく2原色だが霊長類は少しいびつではあるが3原色を獲得している。
天体観測ではガンマ線、X線、紫外線、赤外線、電波を撮影し、波長を少しずらした3成分を合成して無理やり色として人に見せている。
比視感度
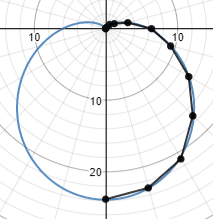
比視感度曲線と適当に選んだ色の明るさを示した(塗り色はsRGB)。
波長による感じる明るさを示したもので、555nmの感度を100%としている
波長による感じる明るさを示したもので、555nmの感度を100%としている
上で適当に選んだ色を数値として比べるとこれだけ差がある
| 波長 nm | 色 | 標準比視感度 | 555nmと同じ明るさに見せる場合の倍率 |
| 360 | 紫(紫外) | 0.000003917 | 25万5千 |
| 410 | 紫 | 0.00121 | 826 |
| 465 | 青 | 0.0739 | 13.5 |
| 490 | 青緑 | 0.20802 | 4.81 |
| 540 | 緑 | 0.954 | 1.05 |
| 570 | 黄 | 0.952 | 1.05 |
| 590 | 橙 | 0.757 | 1.32 |
| 630 | 赤 | 0.265 | 3.77 |
| 720 | 赤 | 0.001047 | 955 |
| 830 | 赤(赤外) | 0.00000045181 | 221万 |
「比視感度」は複数人の平均値から定義されたものだが実際には個人差があり、特に年齢による劣化も大きく20代以降からは短波長側(紫や青)の感度が弱くなっていく。
「暗所視標準比視感度」というものもあるのだが、これはとても暗いところで目が慣れないと見えないくらいの明るさでの視感度である。
完全な「暗所視」では錐体が働かないので色を見ることはできない。
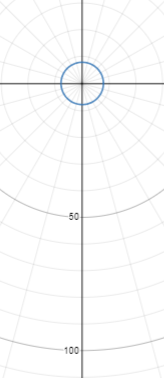
「暗所視」の視感度は全体的に短波長側にシフトし507nmの波長である青緑が一番明るく感じる。
暗所視の視感度を高さを合わせて重ねたもの(実際は暗所視の山の高さは明所視の2.5倍くらい)
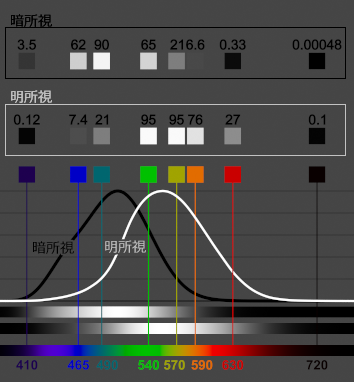
暗所視では青が明るくなり赤が暗くなっていることがわかる
対象物が2[cd/㎡]以上なら「明所視」となり錐体が主に働いている状態。
対象物が0.01[cd/㎡]以下なら「暗所視」となり桿体が主に働いてる状態。
0.01[cd/㎡]の明るさというのは、黒い壁の真っ暗な室内でろうそく一本で照らされた5m先の白い紙を見た時の明るさくらいである。
0.01~2[cd/㎡]の間なら錐体と桿体の両方が働いているので「明所視」と「暗所視」の間の見え方になり「薄明視」と呼ばれる
なぜこのような仕組みが備わっているのか理由はわからないが、日没後の青みのある空のわずかな光でも見ることができるように対応していったのかもしれない。
だんだんと青が明るく感じ、赤が暗く感じるようになり、これをプルキンエ現象と言う。
10ルクスとはどのくらいかというと蝋燭から30cm離れたところが照らされる明るさ。
または太陽が日没から水平線より下に6度沈むまでの間で照らされた屋外明るさのことを「市民薄明(Civil twilight)」と呼ばれているがこの時の明るさも10ルクス位。
そうすると青系と赤系の順位がかなり変わってくるはず。
カラーチェッカーがない場合は色があるものなら何でもよい。

自分の見え方はこのような順位になった

特に一番右の水色は暗所ではかなり明るくなった
全体的に赤系が暗くなり、青系が明るくなっていることが実感できた
日中に室内の照明を全て消し、屋外の光源だけで明所視として観察し、
次はカーテンを閉め、色が見えなくなるくらいのわずかな光にして5分~10分待ち目を暗闇に慣れさせてから暗所視として観察する。
光源を変えないことも重要。
もしRGBが測光量だとしたらどちらも同じ明るさに感じるはずであるが実際はそうではなく
緑のほうが明るく感じる。
レンダリングの数値もこの状態のRGBで行われるので「放射量」でレンダリングしていると考えてよい。
これはレンダリングというよりはモニタ自体が放射量で扱われているから。
その場合は明るさの違いを相殺するRGBの係数が必要になる。
ただし、照明の前に色付きフィルムがあると仮定しその色を指定しているという考えなら、相殺するRGBの係数はいらない。
また色や光を計測する機器の基本は「測光量」なので、発光体の「輝度」や照明の「照度」の計測値を使う場合は「測光量」であることに注意すること。
「光度」はSI基本単位の7個の基本量の1個。
輝度にかんしてはnit(ニト)が使われることも多いが非SI単位。
ANSIルーメンというプロジェクタ用の単位もある。
放射量(Radiometric Quantity)
光束が多いほど密度が上がるため明るいライトということになる。
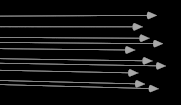
以下は並行光、点光、面光の光束をイメージしたもので、1本の線を1[ルーメン]として表した。
この線の密度で光源から出ている光の強度がわかる。
「明所視」「暗所視」「薄明視」
「比視感度」と言えば「明所視標準比視感度」のことを指すのが普通で、これは明るいところの見え方である。「暗所視標準比視感度」というものもあるのだが、これはとても暗いところで目が慣れないと見えないくらいの明るさでの視感度である。
完全な「暗所視」では錐体が働かないので色を見ることはできない。
「暗所視」の視感度は全体的に短波長側にシフトし507nmの波長である青緑が一番明るく感じる。
暗所視の視感度を高さを合わせて重ねたもの(実際は暗所視の山の高さは明所視の2.5倍くらい)

暗所視では青が明るくなり赤が暗くなっていることがわかる
対象物が2[cd/㎡]以上なら「明所視」となり錐体が主に働いている状態。
対象物が0.01[cd/㎡]以下なら「暗所視」となり桿体が主に働いてる状態。
0.01[cd/㎡]の明るさというのは、黒い壁の真っ暗な室内でろうそく一本で照らされた5m先の白い紙を見た時の明るさくらいである。
0.01~2[cd/㎡]の間なら錐体と桿体の両方が働いているので「明所視」と「暗所視」の間の見え方になり「薄明視」と呼ばれる
なぜこのような仕組みが備わっているのか理由はわからないが、日没後の青みのある空のわずかな光でも見ることができるように対応していったのかもしれない。
プルキンエ現象
照度が10ルクスを下回るくらいから「薄明視」になっていくと言われだんだんと青が明るく感じ、赤が暗く感じるようになり、これをプルキンエ現象と言う。
10ルクスとはどのくらいかというと蝋燭から30cm離れたところが照らされる明るさ。
または太陽が日没から水平線より下に6度沈むまでの間で照らされた屋外明るさのことを「市民薄明(Civil twilight)」と呼ばれているがこの時の明るさも10ルクス位。
暗所視を実感する方法
「明所視」「暗所視」を実感するには例えばカラーチェッカーの色を暗いところと明るいところで見てそれぞれ明るさの順位付けをする。そうすると青系と赤系の順位がかなり変わってくるはず。
カラーチェッカーがない場合は色があるものなら何でもよい。

自分の見え方はこのような順位になった

特に一番右の水色は暗所ではかなり明るくなった
全体的に赤系が暗くなり、青系が明るくなっていることが実感できた
日中に室内の照明を全て消し、屋外の光源だけで明所視として観察し、
次はカーテンを閉め、色が見えなくなるくらいのわずかな光にして5分~10分待ち目を暗闇に慣れさせてから暗所視として観察する。
光源を変えないことも重要。
コンピュータグラフィックスは「放射量」
青(RGB 0,0,1)と緑(RGB 0,1,0)があったとすると、もしRGBが測光量だとしたらどちらも同じ明るさに感じるはずであるが実際はそうではなく
緑のほうが明るく感じる。
レンダリングの数値もこの状態のRGBで行われるので「放射量」でレンダリングしていると考えてよい。
これはレンダリングというよりはモニタ自体が放射量で扱われているから。
コンピュータグラフィックスで扱う照明について
例えば照明の色を緑から青に変えた場合に明るさも維持したいなら「測光量」でライティングをしたほうが良い、その場合は明るさの違いを相殺するRGBの係数が必要になる。
ただし、照明の前に色付きフィルムがあると仮定しその色を指定しているという考えなら、相殺するRGBの係数はいらない。
また色や光を計測する機器の基本は「測光量」なので、発光体の「輝度」や照明の「照度」の計測値を使う場合は「測光量」であることに注意すること。
測光量と放射量の単位の比較表
最初の表が測光量、二つ目の表が放射量であり、項目の並びの順番は同じ意味でそろえた。
測光量(Photometric Quantity)
| 基本量、組立量 | 量記号 | 単位 | ||
| SI基本単位 | 固有の名称を持つSI組立単位 | 他の単位(SI組立単位) | ||
| 光度 luminous intensity | I,(Iv) | cd (Candela カンデラ) | - | lm/sr (ルーメン毎ステラジアン) |
| 輝度 luminance | L,(Lv) | - | - | cd/m2(カンデラ毎平方メートル) |
| 光束 luminous flux | Φ,(Φv) | - | lm (Lumen ルーメン) | cd·sr (カンデラステラジアン) |
| 照度 illuminance | E,(Ev) | - | lx (Lux ルクス) | lm/m2(ルーメン毎平方メートル) |
| 光束発散度 luminous exitance | M,(Mv) | - | - | lm/m2(ルーメン毎平方メートル) |
| 光量 quantity of light 光度エネルギー luminous energy |
Q,(Qv) | - | - | lm·s (ルーメン秒) |
| 露光量 Luminous exposure | H,(Hv) | - | - | lx·s (lルクス秒) |
| 発光効率 luminous efficacy | η | - | - | lm/W (ルーメン毎ワット) |
輝度にかんしてはnit(ニト)が使われることも多いが非SI単位。
ANSIルーメンというプロジェクタ用の単位もある。
| 組立量 | 量記号 | 単位 | ||
| SI基本単位 | 固有の名称を持つSI組立単位 | 他の単位(SI組立単位) | ||
| 放射強度 radiant intensity | I,(Ie) | - | - | W/sr (ワット毎ステラジアン) |
| 放射輝度 radiance | L,(Le) | - | - | W/sr/m2 (ワット毎ステラジアン毎平方メートル) |
| 放射束 radiant flux | Φ,(Φe) | - | W (Watt ワット) | J/s (ジュール毎秒) |
| 放射照度 irradiance | E,(Ee) | - | - | W/m2 (ワット毎平方メートル) |
| 放射発散度 radiant exitance | M,(Me) | - | - | W/m2 (ワット毎平方メートル) |
| 放射エネルギー radiant energy | Q,(Qe) | - | J (Joule ジュール) | m2·kg·s-2 = N・m (ニュートンメートル) |
| 放射露光量 radiant exposure | H,(He) | - | - | J/m2 ( ジュール毎平方メートル) |
| - | - | - | - | - |
光束
光束を一言で言うと光を真っすぐな線で表し、この線の量によって明るさが決まるもの
量 : 光束(こうそく luminous flux)
単位 : lm(ルーメン Lumen)
記号 : Φ または Φv
光束の参考値
光束が多いほど明るく照らせることがわかる
量 : 光束(こうそく luminous flux)
単位 : lm(ルーメン Lumen)
記号 : Φ または Φv
光束の参考値
| 光源 | 光束[lm]の目安 |
| 太陽光 | 36000000000000000000000000000 (3.6*10^28) |
| メタルハライド 1000w | 100000 |
| 高圧ナトリウムランプ400w | 50000 |
| 水銀灯 400w | 20000 |
| 蛍光管 40w | 3000 |
| 白熱灯60w、LED照明10w | 800 |
| 蝋燭 | 10 |
光束はある面を通過する単位時間当たりの光の量。
光束は光度や輝度等の他の単位の基礎となっている。
ライトの明るさは全光束で記載されることが多い。光束の特徴
- 光度や照度などのその他の単位の基になっている
- ライトから出ている明るさを表すことができるが、どの方向にどれだけというのは分かりづらい
ライトの明るさと光束
3個の電球(1個はスポットライト)と小さい蝋燭を同じ露光量で撮影した。光束が多いほど明るく照らせることがわかる
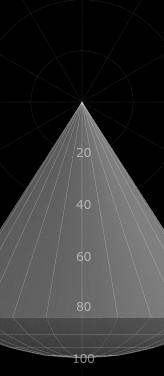
光束のイメージ
光束は一本の線を適当な値として考えるとわかり易い。光束が多いほど密度が上がるため明るいライトということになる。

以下は並行光、点光、面光の光束をイメージしたもので、1本の線を1[ルーメン]として表した。
この線の密度で光源から出ている光の強度がわかる。
光度
光度を一言で言うとその方向にどれだけ光の強度が出ているかを表すもの
量 : 光度(こうど luminous intensity)
単位 : cd(カンデラ Candela)
記号 : Iまたは Iv
光度の参考値
光束の密度をそれぞれの方向で数値化したものが光度。
光度とは単位立体角あたりの光束であり、これは光源が中心にあった場合の半径1mの球の単位面積あたりの光束と考えても良い。
光度は光源の面積を考えない点から出ている光源を想定している。
光度は特定の方向の光束の密度のことなので、「こっちの方向はこれだけ光束が出ていて、あっちにはこれだけ光束が出ている」ということが表せる。これは方向ごとの光の強さを表していることになる。
それを図にしてわかり易くした「配光特性」と言うものがあり、2Dや3Dの極座標で描かれることが多い。
配光特性は光度の分布に使われることが多いが照度や輝度でも使われることがある。
車のヘッドライトの仕様は光束や光度で表示されている。
光束で全体の明るさは何となくわかるかもしれないが、正面がどの程度強く出ているのかは光度を見ないとわからない。
1ステラジアンという立体角の大きさは単純なコーンで表すとこの大きさになる。
立体角Ω (Solid angle) [sr=Steradian=ステラジアン]
全球を4πとした球の面積で立体角を表している。なので単位球の面積=立体角
量 : 光度(こうど luminous intensity)
単位 : cd(カンデラ Candela)
記号 : Iまたは Iv
光度の参考値
| 光源 | 光度[cd]の目安 |
| 太陽光 | 2860000000000000000000000000 (2.86×10^27) |
| ヘッドライト | 10000~ |
| 1000ルーメンの電球(均等) | 80 |
| 蝋燭 | 1 |
光束の密度をそれぞれの方向で数値化したものが光度。
光度とは単位立体角あたりの光束であり、これは光源が中心にあった場合の半径1mの球の単位面積あたりの光束と考えても良い。
光度は光源の面積を考えない点から出ている光源を想定している。
光度は特定の方向の光束の密度のことなので、「こっちの方向はこれだけ光束が出ていて、あっちにはこれだけ光束が出ている」ということが表せる。これは方向ごとの光の強さを表していることになる。
それを図にしてわかり易くした「配光特性」と言うものがあり、2Dや3Dの極座標で描かれることが多い。
配光特性は光度の分布に使われることが多いが照度や輝度でも使われることがある。
車のヘッドライトの仕様は光束や光度で表示されている。
光束で全体の明るさは何となくわかるかもしれないが、正面がどの程度強く出ているのかは光度を見ないとわからない。
光度の特徴
- ライトの強度を方向ごとに表すことができる
- 方向に対しての光束の密度なので距離による変化はない
- 立体角という考えが重要になる
立体角とは
立体角は光度の概念で重要になる。
半径1[m]の球の面積は約12.56㎡であり、これを1㎡に切り取るコーンのことを1[sr:ステラジアン]と言い、これは立体角という角度である。1ステラジアンという立体角の大きさは単純なコーンで表すとこの大きさになる。
平面角θ (Plane angle) [rad=Radian=ラジアン]
1周を2πとした弧の長さで平面角を表している。
平面角は角と円周が結びついている。なので単位円の長さ = 平面角。
立体角はこれの球体版と考え、角と球面が結びついているものである。
全球を4πとした球の面積で立体角を表している。なので単位球の面積=立体角
円錐の頂角Θ(Apex angle)と立体角Ωの関係
Ω = 2π * ( 1 -cos(Θ/2) )
Θ = 2 * arccos( 1 - Ω/(2π) )
半頂角で表すことも多い
単位立体角(1ステラジアン[sr])とその円錐の頂角θ
全方向に均等な点光源の光束 Φ[lm] の光度は Φ/4π[cd]
全方向均一な点光源100[lm]の光度は全方向に約8[cd:カンデラ]である。
100本の線が放射状に出ていき、1mの距離の面の1㎡当たりを通過する光束の数がどの方向も約8本になるので光度はどの方向も8[cd]ということ。


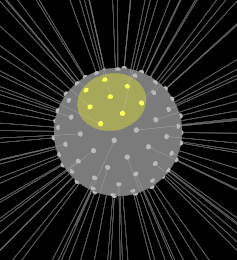
半径1mの球の表面積は12.56[㎡]なので1[㎡]当たりの光束は1/12.56になる。
100ルーメンを丁度1ステラジアンにだけ照射した場合は正面の光度は100[cd]となる。
ただし、正面から35度を超えてしまうと0[cd]になる。
さらに照射する立体角を1/10に絞り0.1[sr]にすると正面は10倍の密度となり1000[cd]となる。
ただし、正面から10.3度を超えてしまうと0[cd]になる
0.1[sr]の中に100本なので 100/0.1 = 1000 ということになる
その方向の微小立体角内の光束を微小立体角で割ったものがその方向の光度ということ。
光度 I = Φ/Ω

この本数から光度に変換するには、
立体角0.05の中の本数なので0.05で割り、1本0.01ルーメンなので0.01を掛けて光度を出した
100本の線が放射状に出ていき、1mの距離の面の1㎡当たりを通過する光束の数がどの方向も約8本になるので光度はどの方向も8[cd]ということ。



半径1mの球の表面積は12.56[㎡]なので1[㎡]当たりの光束は1/12.56になる。
100ルーメンを丁度1ステラジアンにだけ照射した場合は正面の光度は100[cd]となる。
ただし、正面から35度を超えてしまうと0[cd]になる。
さらに照射する立体角を1/10に絞り0.1[sr]にすると正面は10倍の密度となり1000[cd]となる。
ただし、正面から10.3度を超えてしまうと0[cd]になる
1[sr]よりも小さい範囲になっているため、この密度のまま1[sr]だったら1000本になると思えばよい。
これは立体角で割るということでもあり、0.1[sr]の中に100本なので 100/0.1 = 1000 ということになる
その方向の微小立体角内の光束を微小立体角で割ったものがその方向の光度ということ。
光度 I = Φ/Ω
光度の分布と配光特性
緑のグラフは全方向均等な100[lm]なので光度は約8[cd]となっていることがわかる。
青いグラフは正面から真後ろまで徐々に光束が減るタイプのもので同じ100[lm]だが後ろに照射しない分正面が明るくなっている。
イメージしやすいようにあえて光束で表現してみる。
試しに上の青い方の配光特性を1本1[lm]として100本の光束で表すとこんな感じになり、下の方が密度が高い様子がわかる。
これが正しいものかを強引に確認してみることにする。
このままでは精度が悪いのでサンプル数を100倍に増やす。
100倍の1万本にする代わりに1本0.01[lm]とする。
そして黄色で塗った範囲内である0.05[sr]の中に含まれている光束を調べて光度に換算する。
0.05[sr]内にある本数(真下を0度とした場合)

立体角0.05の中の本数なので0.05で割り、1本0.01ルーメンなので0.01を掛けて光度を出した
この光度をプロットしたものが黒いラインなので上で表した光束の作図はほぼ正しいことがわかる
照度
照度を一言で言うとその場所にどれだけの光が当たっているかを表すもの
量 : 照度(しょうど illuminance)
単位 : lx(ルクス Lux)
記号 : Eまたは Ev
照度の参考値
光度は光束がある方向へどのくらいの量が出ているかを示すもので単位立体角当たりの光束であった。
照度は面がどれだけの光束を受けているかを示すもので単位面積当たりに受ける光束である。
1m先の照度は光度と同じ値になる。これは光度の基準である単位立体角は半径1mの1㎡を切り取るコーンだから。
例えば電球の正面の光度が100カンデラだとして、物体が受ける光束の量は1m先では1平方メートル当たり100ルーメンなので照度は100ルクスとなる。
このように目的の場所にどれだけ光が当たっているかを表すのが照度である。
量 : 照度(しょうど illuminance)
単位 : lx(ルクス Lux)
記号 : Eまたは Ev
照度の参考値
| 環境 | 照度[lx]の目安 |
| 太陽光 | 数万~10万 |
| 曇り | 数千~数万 |
| 明るい店内、スタジアム | 1000~2000 |
| オフィス | 500 |
| リビング、ホテルロビー | 100 |
| 市民薄明(日没後少し) | 5 |
| 公園、路地の街灯 | 1~5 |
| 満月明かり | 0.1~0.2 |
| 星明り | 0.001 |
| 暗室 | 0 |
光度は光束がある方向へどのくらいの量が出ているかを示すもので単位立体角当たりの光束であった。
照度は面がどれだけの光束を受けているかを示すもので単位面積当たりに受ける光束である。
1m先の照度は光度と同じ値になる。これは光度の基準である単位立体角は半径1mの1㎡を切り取るコーンだから。
例えば電球の正面の光度が100カンデラだとして、物体が受ける光束の量は1m先では1平方メートル当たり100ルーメンなので照度は100ルクスとなる。
このように目的の場所にどれだけ光が当たっているかを表すのが照度である。
照度の特徴
- 照度は光源からの距離が離れるほど減る(並行光源は含まない)
- 受光面が傾くほど減る特徴がある
光を受ける面が傾くと暗くなる
光の入射が斜めになるほど照度は減る(単位面積当たりの光束が減るということ)
1㎡の面から光束100ルーメンが平行に下に向かって面を照らしているとする。(黄色のライン)
受光面が斜めに光を受けると、受光面の面積が多くなる(黄色の範囲)
そのため受光面の1㎡が受ける光束の量は減ることになる(白の範囲)
この時の光束の量(白い点の数)
傾き0度,30度,60度,85度で見てみると白い点の数は100,87,50,9に減っている。
斜めになると光が当たる面積が増えるので、その代わり単位面積当たりの光束は減ることになるのだが、トータルで見ると受ける光束は減ってはいない。
これは微小面で観察しても同じ理屈。
角度によりどれだけ照度が減るのか。
1㎡の面から光束100ルーメンが平行に下に向かって面を照らしているとする。(黄色のライン)
受光面が斜めに光を受けると、受光面の面積が多くなる(黄色の範囲)
そのため受光面の1㎡が受ける光束の量は減ることになる(白の範囲)
この時の光束の量(白い点の数)
傾き0度,30度,60度,85度で見てみると白い点の数は100,87,50,9に減っている。
斜めになると光が当たる面積が増えるので、その代わり単位面積当たりの光束は減ることになるのだが、トータルで見ると受ける光束は減ってはいない。
これは微小面で観察しても同じ理屈。
角度によりどれだけ照度が減るのか。
このような減衰を「ランベルトの余弦則」という
距離が離れると暗くなる
一般的な光源は放射状に広がる。
そのため遠くに行くほど光束を受ける量は少なくなり、近づくと多くの光束を受ける。
下図は1000カンデラの点光源があり、1㎡の面積が受ける照度の様子
1000カンデラとは単位立体角当たり1000本の光束が出ているということ。
ここでは1ステラジアンの立体角に1000ルーメンの光束を放射し、これを1000本のラインで表した。

1m先の1㎡に1000本当たっているので照度は1000ルクス
2m先では4㎡を照らすことになるので1㎡内には1/4の250本あるので照度は25ルクス
3m先では9㎡を照らすことになるので1㎡内には1/9の111本あるので照度は111ルクス
一般的な光源は距離が遠い所ほど広い面積を照らすので、照度は照らす面積比に反比例する。
例えば1m先を1㎡照らすスポットライトが3m先では2㎡照らせたとすると、3mの時は1mの時の半分の照度ということ。
点光源の場合は球状に広がるので照度は距離の2乗に反比例する。
遠くになると光が当たる面積が増えるので、その代わり単位面積当たりの光束は減ることになるのだが、トータルで見ると受ける光束は減ってはいない。
完全に並行なら距離による照射面積は変わらないので減衰はしないということ(空気中の塵による散乱は考えないとする)
そのため遠くに行くほど光束を受ける量は少なくなり、近づくと多くの光束を受ける。
1000カンデラとは単位立体角当たり1000本の光束が出ているということ。
ここでは1ステラジアンの立体角に1000ルーメンの光束を放射し、これを1000本のラインで表した。

1m先の1㎡に1000本当たっているので照度は1000ルクス
2m先では4㎡を照らすことになるので1㎡内には1/4の250本あるので照度は25ルクス
3m先では9㎡を照らすことになるので1㎡内には1/9の111本あるので照度は111ルクス
一般的な光源は距離が遠い所ほど広い面積を照らすので、照度は照らす面積比に反比例する。
例えば1m先を1㎡照らすスポットライトが3m先では2㎡照らせたとすると、3mの時は1mの時の半分の照度ということ。
点光源の場合は球状に広がるので照度は距離の2乗に反比例する。
遠くになると光が当たる面積が増えるので、その代わり単位面積当たりの光束は減ることになるのだが、トータルで見ると受ける光束は減ってはいない。
完全に並行なら距離による照射面積は変わらないので減衰はしないということ(空気中の塵による散乱は考えないとする)
配光特性の表現
光束100[lm]が以下のような分布だったとする。
光束1[lm]を一本のラインとしてイメージしたもの
光度は下のように表される。各方向の光度の値を長さにした曲線で、正面の光度はそれぞれ7.96, 23.87, 79.58, 100[cd]となる。これは1m先の照度でもある。
各方向の光度の値を色として表現した場合(100[cd]を1.0とした)
中心で縦に切った断面で見た場合の光度を色で表した。この方が感覚的にわかり易い(100[cd]を1.0とした)。
上の画像に対して距離の2乗で割れば照度の分布になる(100[lx]を1.0とした)。
正面方向4m先の照度は左から0.5, 1.49, 4.97, 6.25[lx]となる
正面方向4m先の照度は左から0.5, 1.49, 4.97, 6.25[lx]となる
輝度
輝度を一言で言うとその場所の光がどれだけ目に入ってくるかを表すもの
量 : 輝度(きど luminance)
単位 : cd/㎡(カンデラ毎平方メートル)
記号 :Lまたは Lv
輝度の参考値
輝度は着目点がどのような明るさに見えるのかを表したもの。
面積を持った光源の表面の明るさを表す場合に使うことが多いが、物体が光を反射した結果の明るさに対しても使われる。
同じ照度で照らされていても黒い物体は反射率が低いので輝度は低くなり、白い物体は反射率が高いので輝度は高くなる。
カメラはピクセルごとに輝度を撮影していると言っても良い。
ディスプレイはピクセルごとに輝度を表示していると言っても良い。
人の目は視細胞ごとに輝度を感じていると言っても良い。
光を受けたすべてのものが、それぞれの場所から反射し二次光源として振る舞い、その光源が目に入ってくる。
輝度は二次光源でもあるので光度で表現したくなるのだが、光度は面積を持たない概念なので「面積を考慮した光度」というものが輝度である。
そして輝度の説明では均等拡散とか完全拡散とかがよく出てくる。
輝度は単位面積から発している光度と定義されているのだが、単位面積というよりは単位投影面積といったほうがわかり易い。
輝度の概念は難しそうに感じるが、人が見ることのできるものなので扱いやすく直感的な単位である
均等拡散面の場合は微小面の見かけの面積はcos(θ)で減っていくが密度は1/cos(θ)で増えていくので完全に相殺される。
下の図は左から法線方向に0,60,70度と傾いた時の光度と見かけの密度を表した。
それぞれ密度が1,2,3倍と増えている。
微小面の見かけの範囲内の黄色い線で表した光度を全て足すと長さが同じになるので見かけの光度が一定になる。これが輝度が一定となるということ。
乳白色な面をもつライトを点灯し正面から撮影した。
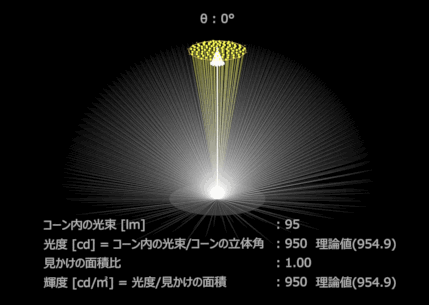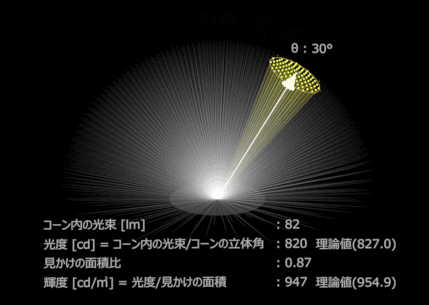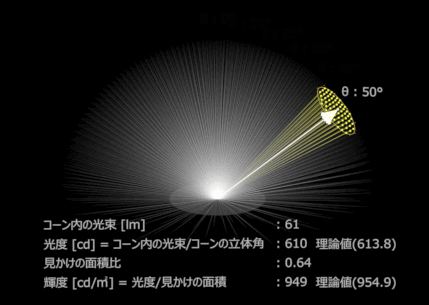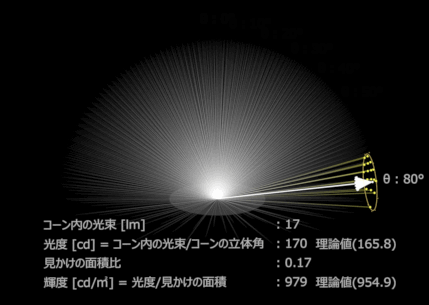
グレージング角ほど光度は減っている。(黄色コーンの中の光束の数)
これは見かけの面積が減っているからでもあるのだが、輝度に関しては、見かけの面積で減っているのを無かったことにするので、光度を見た目の面積比で割ってしまう。
輝度は1平方メートル当たりの光度なので、ここでは発光面積が1㎡なので1で割った値が輝度となる。発光面積が0.1㎡なら0.1で割った値が輝度となり、10倍の輝度となる。
左から8,12.33,18.5EVで撮影した。中央は左の1/20、右は中央の1/70の露光量となる
一点から並行に照らされた光が面で反射するとき、鏡にように方向と強度をそのまま跳ね返した場合は光の広がりによる減衰もなくもちろん距離による減衰もない。
完全拡散反射であるランバート反射では入ってきた光を放射状に反射する。
但し裏面から見たら表面が見えないため裏側には光を照らすことはできないので半球に広がることが想像でき、半球に均等に広がった場合は2πで広がることになる(球は4πに広がるので)。
さらにグレージング角では、光度が減るので、これを考慮すると実は光の広がる量はがさらに半分になるので2πではなくてπで広がることになる。
半球を細かく分割して考えてみる
半球を立体角で表すと2πである(半径1の半球の面積でもある)。
これを100分割したコーンで表してみる。
一個のコーンの立体角は半球の100分割なので2π/100 ≒ 0.0628[sr]。

これが100個集まれば当たり前だが2πである。
正面の見かけの面積比を1.0とすると横では0になり、これは法線方向に対してcos(θ)の値になる。
cos(θ)の値はそれぞれこんな感じになる

ちなみにこのcos(θ)の平均は0.5となる。
コーンの立体角(面積でもある)にcos(θ)を掛けるとそれぞれこのような感じになる

これを全て足し合わせるとπになる
このことから完全拡散反射の広がりは全体でπに広がるので反射光はπで割った値となる。
これは完全拡散反射は照度をπで割ったものが輝度になるということ。
基本単位に光度[cd]が定義されているが、本当は光束[lm]にしたかったらしい
https://www.jstage.jst.go.jp/article/bunkou1951/29/2/29_2_127/_pdf/-char/ja
1995年に無次元量の平面角ラジアン「rad」や立体角ステラジアン「sr」も無次元の単位として組立単位に正式に加わった。
以前は補助単位とされていたが、補助単位は廃止された。
https://ja.wikipedia.org/wiki/SI%E7%B5%84%E7%AB%8B%E5%8D%98%E4%BD%8D
量 : 輝度(きど luminance)
単位 : cd/㎡(カンデラ毎平方メートル)
記号 :Lまたは Lv
輝度の参考値
| 環境 | 輝度[cd/㎡]の目安 |
| 太陽 | 16億 |
| フィラメント | 数百万 |
| 白熱灯 | 数万 |
| 蛍光灯 | 数千~数万 |
| 空 | 数千 |
| 太陽に近い場所の青空 | 数万以上 |
| 月 | 2500 |
| 明るいテレビの白 | 1000 |
| 一般的なPCモニタの黒 | 0.1~1 |
輝度は着目点がどのような明るさに見えるのかを表したもの。
面積を持った光源の表面の明るさを表す場合に使うことが多いが、物体が光を反射した結果の明るさに対しても使われる。
同じ照度で照らされていても黒い物体は反射率が低いので輝度は低くなり、白い物体は反射率が高いので輝度は高くなる。
カメラはピクセルごとに輝度を撮影していると言っても良い。
ディスプレイはピクセルごとに輝度を表示していると言っても良い。
人の目は視細胞ごとに輝度を感じていると言っても良い。
光を受けたすべてのものが、それぞれの場所から反射し二次光源として振る舞い、その光源が目に入ってくる。
輝度は二次光源でもあるので光度で表現したくなるのだが、光度は面積を持たない概念なので「面積を考慮した光度」というものが輝度である。
そして輝度の説明では均等拡散とか完全拡散とかがよく出てくる。
輝度は単位面積から発している光度と定義されているのだが、単位面積というよりは単位投影面積といったほうがわかり易い。
輝度の概念は難しそうに感じるが、人が見ることのできるものなので扱いやすく直感的な単位である
輝度の特徴
- 同じ明るさの照明の場合は発光部が小さいほど輝度が高くなる
- 均等拡散面の場合は観測する角度による変化はない
- 完全拡散反射の場合は輝度は照度の1/πの値になる
- 観測距離による変化はない
均等拡散、完全拡散とは
輝度の概念を表す場合に都合の良い理想的な拡散面モデルとしてよく使われるもの。
完全拡散面の配光特性

微小面に着目すると、法線方向に光束の密度(光度)が多く、グレージング角になると光束が出なくなる。これはグレージング角では見かけの面積が減るからである。
* グレージング角grazing angle(仰角)とは「擦れ擦れな角度」という意味。
このように微小面はグレージング角では光度が減るのだが、実際には面の面積があるのでグレージング角で見えている微小面は隣の領域まで見えてしまうため密度が増すことになり、光度は減っていないため人の目には一定の明るさに見えることになるのだが、これを輝度という。
ライトの角度と完全拡散面の配光特性

微小面に着目すると、法線方向に光束の密度(光度)が多く、グレージング角になると光束が出なくなる。これはグレージング角では見かけの面積が減るからである。
* グレージング角grazing angle(仰角)とは「擦れ擦れな角度」という意味。
このように微小面はグレージング角では光度が減るのだが、実際には面の面積があるのでグレージング角で見えている微小面は隣の領域まで見えてしまうため密度が増すことになり、光度は減っていないため人の目には一定の明るさに見えることになるのだが、これを輝度という。
ライトの角度と完全拡散面の配光特性
こちらは立体で表した。
ライトがグレージング角で照らされていくと照度が減り、照度に比例して光度や輝度も減る。
斜めからライトが当たったとしても一番光束が出る方向は法線方向なのは変わらない。
レフ版の面を被写体に向けるのもそれが理由。
反射光が法線に対してcosθの値になるものを理想的な拡散反射とされ、「均等拡散反射」という。
均等拡散反射でも反射率が100%の真っ白なものを「完全拡散反射」という。
現実に同じ特性を持つものはないといわれているが、計測器などの校正で使われる標準白色版は完全拡散に近く、反射率が99%のものも存在している。
輝度の観点から見ると均等拡散面とはどの方向から見ても輝度が変わらない特性となる。
ちなみにTVモニタは見る角度により輝度が変わるものが多く、正面にから見ると輝度が高く、横のから見ると輝度が低い傾向にあるので均等拡散面ではない。均等拡散面の輝度は観測する角度で変化しない
下図は面の輝度が一定の均等拡散面の光源があり、それぞれの場所での発光面の見え方を表した。
観測する角度が変わっても発光面の明るさは変わっていない。
ただし、発光面の見た目の大きさは変わっていて、これが意味するのはその場所に届く光の量が減るということ。
観測方向が横になるにつれて、輝度は減っていないが発光面の見た目の大きさが減っているので光度や照度が減っていると言える。
輝度は観測距離で変化しない
観測する距離も同じで、観測者が離れても発光面の輝度は変わらないが、発光面の見た目は小さくなるのでその場所に届く光の量は減っているので照度が減っていると言える(光度は減っていない)
発光面を徐々に離れて撮影した。(3枚とも露光量は同じ)
当たり前だけど発光面の輝度は変化していないが離れるにつれて小さく写っている。
角度や距離によって光束が減っているのに輝度は減っていないというのは不思議に感じるがこれは目でピントを合わせているからできることである。
白い紙と鏡の違いをイメージするとわかるかもしれない。
なぜ斜めから見ても輝度が変わらないのか
グレージング角になっていくと密度が上がるから。
面の光度がグレージング角で弱くなるのは全体の見た目の面積が小さくなるから。
しかし、面の一部だけを見た時はグレージング角で密度が上がっていく。
均等拡散面の場合は微小面の見かけの面積はcos(θ)で減っていくが密度は1/cos(θ)で増えていくので完全に相殺される。
下の図は左から法線方向に0,60,70度と傾いた時の光度と見かけの密度を表した。
それぞれ密度が1,2,3倍と増えている。
微小面の見かけの範囲内の黄色い線で表した光度を全て足すと長さが同じになるので見かけの光度が一定になる。これが輝度が一定となるということ。
乳白色な面をもつライトを点灯し正面から撮影した。
端の方でもそれほど輝度は減っていないことから、均等拡散透過に近いと言えるかもしれない
完全拡散面の光束と光度と輝度のイメージ
面積1㎡の均等拡散している面が光束3000[lm]を放出したとして、0.1[sr]のコーン内の光束を調べて、輝度を観測する様子を表したもの
グレージング角ほど光度は減っている。(黄色コーンの中の光束の数)
これは見かけの面積が減っているからでもあるのだが、輝度に関しては、見かけの面積で減っているのを無かったことにするので、光度を見た目の面積比で割ってしまう。
輝度は1平方メートル当たりの光度なので、ここでは発光面積が1㎡なので1で割った値が輝度となる。発光面積が0.1㎡なら0.1で割った値が輝度となり、10倍の輝度となる。
発光面積が小さい照明は輝度が高い
徐々に暗く撮影した画像。発光部分は輝度がかなり高いことがわかる。左から8,12.33,18.5EVで撮影した。中央は左の1/20、右は中央の1/70の露光量となる
発光面積が大きい照明は輝度が低い
こちらも同じEV値で撮影している。一番右はほぼ何も見えない
シーリングライトのように大きな発光面になると輝度は抑えられ、影も柔らかくなる。
間接照明も大きな面で拡散させ、面積を稼ぐことで輝度の低いやわらかい照明になる。
光束を発光面の輝度に変換する例
後日記載
拡散反射とπの関係
CGのライティングで白い板が1.0にレンダリングされるためには並行光源を3.14にしていることが多いと思うがその場合はこれが理由となっている。
例えば100[lx]で照らされている100%反射の白い紙の輝度は31.85[cd/㎡]である。
完全拡散反射であるランバート反射では入ってきた光を放射状に反射する。
但し裏面から見たら表面が見えないため裏側には光を照らすことはできないので半球に広がることが想像でき、半球に均等に広がった場合は2πで広がることになる(球は4πに広がるので)。
さらにグレージング角では、光度が減るので、これを考慮すると実は光の広がる量はがさらに半分になるので2πではなくてπで広がることになる。
半球を細かく分割して考えてみる
半球を立体角で表すと2πである(半径1の半球の面積でもある)。
これを100分割したコーンで表してみる。
一個のコーンの立体角は半球の100分割なので2π/100 ≒ 0.0628[sr]。

これが100個集まれば当たり前だが2πである。
正面の見かけの面積比を1.0とすると横では0になり、これは法線方向に対してcos(θ)の値になる。
cos(θ)の値はそれぞれこんな感じになる

ちなみにこのcos(θ)の平均は0.5となる。
コーンの立体角(面積でもある)にcos(θ)を掛けるとそれぞれこのような感じになる

これを全て足し合わせるとπになる
このことから完全拡散反射の広がりは全体でπに広がるので反射光はπで割った値となる。
これは完全拡散反射は照度をπで割ったものが輝度になるということ。
輝度と光度の関係は投影面積が重要
ある輝度の発光面の面積が増えると光束や光度は上がる。
例えばPCモニタを10台並べたら全光束は増えて部屋が明るくなる。
光束や光度を保ちつつ発光面積を増やす場合は輝度を減らす
例えばPCモニタの輝度を1/10にしてから10台並べたら光束は変わらない。
光度を保つためには面積が増えた分だけ輝度を減らすということなので光度を面積で割ればよさそうなことは想像がつく。
面積100倍なら輝度を1/100にすることで照明自体明るさ(光束)は一定になる
例えばPCモニタを10台並べたら全光束は増えて部屋が明るくなる。
光束や光度を保ちつつ発光面積を増やす場合は輝度を減らす
例えばPCモニタの輝度を1/10にしてから10台並べたら光束は変わらない。
光度を保つためには面積が増えた分だけ輝度を減らすということなので光度を面積で割ればよさそうなことは想像がつく。
面積100倍なら輝度を1/100にすることで照明自体明るさ(光束)は一定になる
実は面積で割るのではなく投影面積で割ることが重要。
上の場合は平面なので表面積と投影面積も変わらないので問題ないのだが、
発光体が球体の場合だと、表面積と投影面積に差が出てくる。
ここから続きはまた後で記述します
SI単位について
詳細は https://ja.wikipedia.org/wiki/SI%E7%B5%84%E7%AB%8B%E5%8D%98%E4%BD%8D
「SI」とは「国際単位系」と呼ばれるものでフランス語の「SystemeInternational d′Unites」の略
なので「SI単位」とは「国際単位系の単位」という意味
メートルやキログラムはSI単位で、フィートやポンドはSI単位ではない。
照度の意味を表す単位に、ルクス(lx)、フート・カンデラ(ft-cd)2種類が存在し、前者がSI単位。
照度は単位面積当たりの光束なので、ルクスの場合1平方メートル当たりになるが、フート・カンデラの場合は1平方フィート当たりとなるので数値は約10倍違うものとなる。
SI基本単位
全7個 : 長さ(メートルm)、質量(キログラムkg)、時間(秒s)、電流(アンペアA)、熱力学温度(ケルビンK)、物質量(モルmol)、光度(カンデラcd)基本単位に光度[cd]が定義されているが、本当は光束[lm]にしたかったらしい
https://www.jstage.jst.go.jp/article/bunkou1951/29/2/29_2_127/_pdf/-char/ja
組立単位
この基本単位の組み合わせで作ることができる単位が「組立単位」という。たとえば速度の単位はメートル毎秒[m/s]固有の名称を持つSI組立単位
全22個 : よく使われる「組立単位」を別の名称として記号が与えれれている。例えばm·kg·s-2のことをニュートン「N」として別名の記号を与えている。1995年に無次元量の平面角ラジアン「rad」や立体角ステラジアン「sr」も無次元の単位として組立単位に正式に加わった。
以前は補助単位とされていたが、補助単位は廃止された。
https://ja.wikipedia.org/wiki/SI%E7%B5%84%E7%AB%8B%E5%8D%98%E4%BD%8D
SI併用単位
SIと併用される単位
時間(分min,時h,日d) 平面角(度°,分',秒'') 面積(ヘクタールha) 体積(リットルL) 質量(トンt) 長さ(天文単位au)
SIとの併用が認められている単位
エネルギー(電子ボルトeV) 質量(ダルトンDa) 質量(統一原子質量単位u) 比の対数(ネーパNp) 比の対数(ベルB) 比の対数(デシベルdB)